Curvas de Bezier

 

Historia

Las curvas de Bézier fueron publicadas por primera vez en 1962 por el ingeniero francés Pierre Bézier y posteriormente, trabajando en la Renault, las usó con abundancia en el diseño de las diferentes partes del automóvil. Las curvas fueron desarrolladas por Paul de Casteljau usando el algoritmo que lleva su nombre. Se trata de un método numéricamente estable para evaluar las curvas de Bézier.    Posteriormente, los inventores del PostScript, lenguaje que permitió el desarrollo de sistemas de impresión de alta calidad desde el ordenador, introdujeron en ese código el método de Bézier para la generación del código de las curvas y los trazados. El lenguaje PostScript sigue empleándose ampliamente y se ha convertido en un estándar de calidad universal; por ello, los programas de diseño vectorial como Adobe Illustrator, el extinto Macromedia FreeHand y Corel Draw, tres de los programas más importantes de dibujo vectorial y otros como Inkscape, denominan «bézier» a algunas de sus herramientas de dibujo, y se habla de «trazados bézier», «pluma bézier», «lápiz bézier», etc. Su facilidad de uso la ha estandarizado en el diseño gráfico, extendiéndose también a programas de animación vectorial, como Adobe Flash, y retoque fotográfico , como Photoshop y Gimp, donde se usa para crear trazos, formas cerradas o selecciones. La idea de definir geométricamente las formas no es demasiado compleja: un punto del plano puede definirse por coordenadas. Por ejemplo, un punto A tiene unas coordenadas (x₁, y₁) y a un punto B le corresponde (x₂,y₂). Para trazar una recta entre ambos basta con conocer su posición. Si en lugar de unir dos puntos con una recta se unen con una curva, surgen los elementos esenciales de una curva Bézier; los puntos se denominan «puntos de anclaje» o «nodos». La forma de la curva se define por unos puntos invisibles en el dibujo, denominados «puntos de control», «manejadores» o «manecillas».

pluma bézier

La pluma es una de las herramientas más potentes, precisas y versátiles que podemos aprender en Photoshop. Gracias a ella somos capaces de dibujar trazos simples, crear estelas o siluetear de la forma más precisa posible la cara de una modelo

Curvas cúbicas de Bézier

Curva cúbica de Bézier donde se aprecian los puntos o nodos de anclaje P₁ y P₂

Cuatro puntos del plano o del espacio tridimensional, P₀, P₁, P₂ y P₃ definen una curva cúbica de Bézier. La curva comienza en el punto P₀ y se dirige hacia P₁ y llega a P₃ viniendo de la dirección del punto P₂. Usualmente, no pasará ni por P₁ ni por P₂. Estos puntos solo están ahí para proporcionar información direccional. La distancia entre P₀ y P₁ determina «qué longitud» tiene la curva cuando se mueve hacia la dirección de P₂ antes de dirigirse hacia P₃.

La forma paramétrica de la curva es:

${\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}(1-t)^{3}+3\mathbf {P} _{1}t(1-t)^{2}+3\mathbf {P} _{2}t^{2}(1-t)+\mathbf {P} _{3}t^{3}{\mbox{ , }}t\in [0,1].}$

Los modernos sistemas de imágenes como PostScript, Asymptote y Metafont usan curvas de Bézier desdobladas, compuestas por curvas cúbicas de Bézier para dibujar las formas de las curvas.

Construcción de curvas de Bézier

Curvas lineales

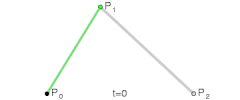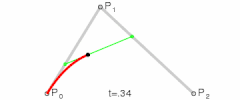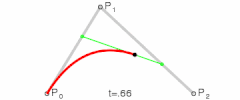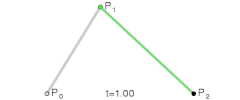
La ${\displaystyle t}$ en la función para la curva lineal de Bézier se puede considerar como un descriptor de lo lejos que está ${\displaystyle B(t)}$ de ${\displaystyle P_{0}}$ a ${\displaystyle P_{1}}$. Por ejemplo cuando ${\displaystyle t=0.25}$, ${\displaystyle B(t)}$ es un cuarto de la longitud entre el punto ${\displaystyle P_{0}}$ y el punto ${\displaystyle P_{1}}$. Como ${\displaystyle t}$ varía entre 0 y 1, ${\displaystyle B(t)}$ describe una línea recta de ${\displaystyle P_{0}}$ a ${\displaystyle P_{1}}$.

Curvas cuadráticas

Para curvas cuadráticas se pueden construir puntos intermedios desde ${\displaystyle Q_{0}}$ a ${\displaystyle Q_{1}}$ tales que ${\displaystyle t}$ varía de 0 a 1: Punto ${\displaystyle Q_{0}}$ varía de ${\displaystyle P_{0}}$ a ${\displaystyle P_{1}}$ y describe una curva lineal de Bézier. Punto ${\displaystyle Q_{1}}$ varía de ${\displaystyle P_{1}}$ a ${\displaystyle P_{2}}$ y describe una curva lineal de Bézier. Punto ${\displaystyle B(t)}$ varía de ${\displaystyle Q_{0}}$ a ${\displaystyle Q_{1}}$ y describe una curva cuadrática de Bézier.

Curvas de órdenes superiores[editar]

Para curvas de orden superior se necesitan, lógicamente, más puntos intermedios. Para curvas cúbicas se pueden localizar puntos intermedios Q0, Q1 y Q2 que describen las curvas lineales de Bézier y los puntos R0 y R1 que describen las curvas cuadráticas:

Y para curvas de grado 4, se pueden localizar los puntos intermedios Q0, Q1, Q2 y Q3 que describen las curvas lineales de Bézier, los puntos R0, R1 y R2 que describen las curvas cuadráticas y los puntos S0 y S1 que describen las curvas cúbicas.

Aplicaciones

Gráficos de ordenador

Las curvas de Bézier han sido ampliamente usadas en los gráficos generados por ordenador para modelado de curvas suaves. Como la curva está completamente contenida en la envolvente convexa de los puntos de control, dichos puntos pueden ser visualizados gráficamente sobre el área de trabajo y usados para manipular la curva de una forma muy intuitiva. Las transformaciones afines tales como traslaciones y rotaciones pueden ser aplicadas, con gran facilidad, a las curvas, aplicando las transformaciones respectivas sobre los puntos de control.

Las curvas cuadráticas y cúbicas son muy corrientes. Las curvas de grados superiores son más difíciles de evaluar. Cuanto más complejas son las superficies que se necesitan, las curvas de bajo orden son menos apropiadas. Para garantizar la suavidad de las curvas el punto de control en el que se juntan dos curvas y el punto de control sobre cualquiera de los lados debe ser colineal. Esta opción está frecuentemente desactivada en programas como Adobe Illustrator o Inkscape. Estas curvas poli-Bézier pueden ser observadas en el formato de archivo SVG.

El método más simple para rasterizar una curva de Bézier es evaluarla en muchos puntos espaciados, muy próximos entre sí, y escanearla aproximando la secuencia de segmentos lineales.

Esta manera de proceder no garantiza un resultado con la suficiente suavidad porque los puntos pueden estar espaciados demasiado separados. A la inversa, se pueden generar bastantes puntos de control en áreas donde la curva está cercana a la forma lineal.

Un método adoptado, muy común, es la subdivisión recursiva, en el que los puntos de control de la curva son ajustados para ver si la curva se aproxima a segmentos lineales sin pequeñas tolerancias. Si esto no se logra, la curva es subdividida paramétricamente en dos segmentos ${\displaystyle 0\leq t\leq 0.5}$ y ${\displaystyle 0.5\leq t\leq 1}$ y el mismo procedimiento se aplica por recursividad a cada mitad.

También hay métodos que usan la diferenciación, pero se debe tener cuidado y analizar los errores de propagación. Los métodos analíticos donde un desdoble es intersecado con cada línea escaneada hallando raíces de polinomios de grado tres (por segmentación cúbica) y con múltiples raíces, pero no son frecuentes en la práctica.

The Bezier Game